Difference between revisions of "BiologicalUnit"
Jump to navigation
Jump to search
m (moved ManualSymExp to BiologicalAssembly: Wong title.) |
|
(No difference)
| |
Revision as of 11:17, 16 April 2010
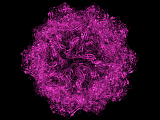
This script can be used to re-create biological units for proteins. (This was created as a workaround of PyMOL's semi-functioning Symexp command.) It's also a fun script to play with for learning about symmetry.
Usage
symMat = readSymmetry("/path/to/some/pdbFile.pdb","pdbFile")
manualSymExp("mates", "pdbFile", symMat)
The Code
#
# Jason Vertrees <Jason-dot-Vertrees-at-schrodinger_dot_com>, 2010.
#
import string
import pymol
from pymol import cmd
def readSymmetry(inFile, verbose=None):
"""
This function will read "inFile" and glean the
symmetry operations, if any, from it.
PARAMS
inFile
(string) path to PDB file
verbose
(boolean) if verbose is not None, print more
RETURNS
matrix
Array of lists. One 16-element list per symmetry operation. Feed this matrix
into manualSymExp in order to make the other symmetry mates in the biological unit
"""
# a remark-350 lines has:
# REMARK 350 BIOMTn TAGn X Y Z Tx
REM, TAG, BIOMT, OPNO, X, Y, Z, TX = range(8)
thePDB = open(inFile, 'rb').readlines()
matrices = []
curTrans = -1
# The transformation is,
# output = U*input + Tx
for l in thePDB:
tokens = string.split(l)
if len(tokens)!=8:
continue
if tokens[REM]=="REMARK" and tokens[TAG]=="350" and tokens[BIOMT].startswith("BIOMT"):
if tokens[OPNO]!=curTrans:
# new transformation matrix
matrices.append([])
matrices[-1].append( map( lambda s: float(s), tokens[X:]))
curTrans = tokens[OPNO]
if verbose!=None:
print "Found %s symmetry operators in %s." % (len(matrices), inFile)
return matrices
def manualSymExp(prefix, objSel, matrices ):
"""
Manually expands the object in "objSel" by the symmetry operations provided in "matrices" and
prefixes the new objects with "prefix".
PARAMS
prefix
(string) prefix name for new objects
objSel
(string) name of object to expand
matrices
(list of 16-element lists) array of matrices from readSymmetry
RETUNRS
None
SIDE EFFECTS
Creates N new obects each rotated and translated according to the symmetry operators, where N
equals len(matrices).
"""
for m in matrices:
n = cmd.get_unused_name(prefix)
cmd.create(n, objSel)
s1 = "%s + (x*%s + y*%s + z*%s)" % (m[0][3], m[0][0], m[0][1], m[0][2])
s2 = "%s + (x*%s + y*%s + z*%s)" % (m[1][3], m[1][0], m[1][1], m[1][2])
s3 = "%s + (x*%s + y*%s + z*%s)" % (m[2][3], m[2][0], m[2][1], m[2][2])
cmd.alter_state(1, n, "(x,y,z) = (%s, %s, %s)" % (s1, s2, s3) )
cmd.extend("readSymmetry", readSymmetry)
cmd.extend("manualSymExp", manualSymExp)
Notes
This is slow compared to Symexp; use the above for learning, playing and when Symexp doesn't work as advertised.