MtsslTrilaterate
| Type | PyMOL Plugin |
|---|---|
| Download | plugins/mtsslTrilaterate.py |
| Author(s) | Dinar Abdullin |
| License | - |
| This code has been put under version control in the project Pymol-script-repo | |
mtsslTrilaterate
mtsslTrilaterate is a PyMOL plugin for the trilateration of objects based on distance restraints.
The mtsslTrilaterate program calculates the coordinates of an object which is defined by the distances from this object to several "reference" objects. The idea of the program is similar to the Global Positioning System (GPS) that can locate an object on the surface of the Earth by measuring distances to a number of GPS-satellites. Applied to biomolecules, this program can be used to localize paramagnetic metal ions in a biomolecular structure by measuring the distances between these ions and artificially attached spin labels.
The mtsslTrilaterate program is a python code and it works as a plugin for the PyMOL program. It is a part of the mtsslSuite package and is optimized to work in pair with the program mtsslWizard.
The program was tested on the 64-bit Windows 7 platform. Due to some problems with the wx library in PyMOL, the program temporarily does not work on the Mac platform.
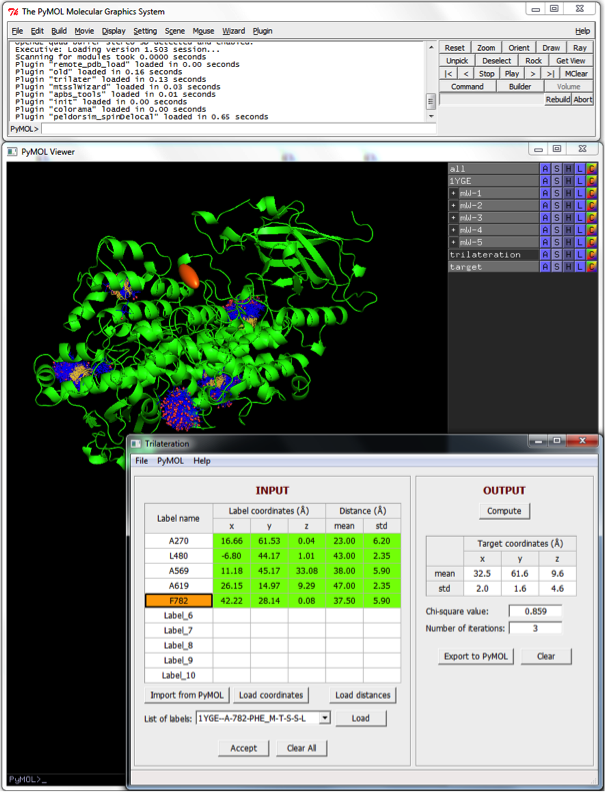
Screen Shot
Installation
1. The program requires python 2.7 (or higher) to be installed. It can be downloaded free of charge from official web site http://www.python.org/.
2. The program also uses wx and numpy libraries. If the basic version of python does not contain these libraries, they should be installed subsequently (e.g. from http://www.lfd.uci.edu/~gohlke/pythonlibs/).
3. The program requires PyMOL version compatible with python 2.7 (or higher).
4. Save the mtsslTrilaterate.py file somewhere in your computer.
5. Run PyMOL. In the "Plugin menu" select "Plugin Manager". Then open the "Install New Plugin" page and click on "Choose file". Select the mtsslTrilaterate.py file. If installation is finished successfully, a message “Plugin Trilateration has been installed” would appear.
6. Run mtsslTrilaterate from the Plugin menu.
Operation Guidelines
The graphical user interface of mtsslTrilaterate is shown above. It consists of a small menu and a main working window. The main window contains two panels called "INPUT" and "OUTPUT", which display the input and output data of the program, correspondingly.
All input data is introduced into the table of the "INPUT" panel. Each row of this table corresponds to one of the spin labels (reference objects) attached to a biomolecule. The user-defined identifiers of these labels are listed in the first column of the table. The following three columns correspond to the Cartesian coordinates (x, y, z) of the labels in the coordinate frame of a biomolecule. The last two columns represent the mean value and the standard deviation of the distance between each label and a target.
The "OUTPUT" panel displays the calculated coordinates of the target and their standard errors.
In the following the step-by-step instruction of using the program is given:
- Load the structure or structural model of a biomolecule to PyMOL. It can be done either in PyMOL selecting "File" → "Open" or in mtsslTrilaterate selecting "PyMOL" → "Load structure to PyMOL".
- Load/create the models of spin labels (reference objects). The models of several commonly used EPR spin labels can be created by means of the mtsslWizad plugin (see http://pymolwiki.org/index.php/MtsslWizard).
- The coordinates of the created spin labels can be entered into mtsslTrilaterate in three different ways:
1) They can be typed manually into the table of the "INPUT" panel.
2) If MTSSL (or MTSL) is used as a spin label and its model is created by means of the mtsslWizard plugin, the coordinates can imported into mtsslTrilaterate automatically by pushing the "Import from PyMOL" button, than choosing the label in the "List of labels" list and pressing the "Load" button. Due to the intrinsic flexibility of MTSSL, the coordinates averaged over all generated conformers will be calculated and used by the program.
3)
- Load biomolecule structure to current PyMOL session. It can be done either in PyMOL selecting File → Open or in mtsslTrilaterate selecting PyMOL → Load structure to PyMOL.
- Create spin labels by means of mtsslWizard selecting in PyMOL Wizard → mtsslWizard. This wizard performs site-directed spin labelling in silico (look http://pymolwiki.org/index.php/MtsslWizard for more information).
- The coordinates of the selected label can be entered in three different ways. Firstly, they can be entered manually to the table. Secondly, the parameters related to a particular spin label can be imported from the current PyMOL session by pushing the “Import from PyMOL” button. The identifiers and average coordinates of spin labels that were generated inside PyMOL beforehand are in this way imported into the program and can be assigned to rows in the data table. Thirdly, the label coordinates can be loaded from an ASCII data file by selecting the label in the table and then clicking the “Load coordinates” button. The data file should contain 3 columns corresponding to x, y, z coordinates. If the label is flexible (i.e. has a set of the coordinates) an average label coordinates will be calculated after loading the data file.
- The distance between the selected label and the target can be entered manually to the corresponding fields of the table or loaded from an ASCII data file clicking the “Load distances” button. This way an interspin distance distribution generated within the DeerAnalysis program (Jeschke, G.; Chechik, V.; Ionita, P.; Godt, A.; Zimmermann, H.; Banham, J.; Timmel, C. R.; Hilger, D.; Jung, H. Appl. Magn. Reson. 2006, 30, 473) can be imported to the program.
- If all input data entered press “Accept” button. At this stage the program checks if at least four spin labels were described completely. Four spin labels is a minimal number of labels that allows to solve the trilateration problem.
- Click “Compute” button. After calculations, the coordinates of the target and their standard deviations should appear in the “OUTPUT” panel. The program also displays an obtained χ2 value and a number of iterations which was required to reach this χ2 value.
Push Export to PyMOL button to get a graphical representation of trilateration in the current PyMOL session. Two PyMOL objects, called “trilateration” and “target”, will be created inside PyMOL (Figure 1). *The “trilateration” object represents a ‘trilateration-sphere’ plotted around each used spin label. The radius of each sphere equals to the average distance between the corresponding spin label and the unlocalized spin center. The space where these spheres intersect each other determines the location of the spin center. This space is depicted by the “target” ellipsoid. The center of the ellipsoid corresponds to the most probable coordinates of the spin center, whereas the legths of its semi-principal axes equal to the obtained standard errors of these coordinates. The scale of semi-principal axes, i.e. the confidence level of the solution, can be incresed in the File → Preferences → Output panel.
- Click “Save as” button or select File → Save as in the File menu to save current section as a ASCII data file. Afterwards this session can be reinitialized by opening this data file through File → Open.
The “OUTPUT” panel is used to displays the results of the trilateration process. After the calculation is started by pushing the “Compute” button, the program solves the trilateration problem and displays the most probable coordinates of the target and their standard errors.
The File menu contains the Open, Save as, and Close commands to work with data files. It also incorporates the Preferences window which allows user to format the input and output data of the program as well as to adjuxt some calculation parameters.
The PyMOL menu allows user to open and close the PyMOL data files within the program.
Reference
If you find this program useful, please cite this paper:
It also contains detailed information about the program and examples of its application.
Contact
Dinar Abdullin
abdullin@pc.uni-bonn.de
Acknowledgement
Thanks to Jason Vertrees and Thomas Holder for some programming tips.