AngleBetweenHelices

• 
• 

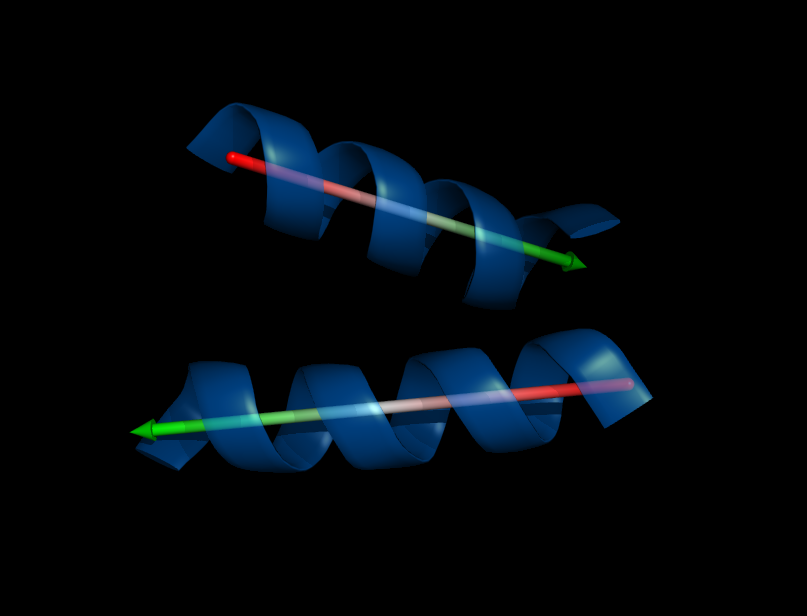
Calculate angle between alpha-helices or beta-sheets. There are four different methods implemented to fit a helix, two of them also work for sheets or loops.

Commands

helix_orientation selection [, visualize [, sigma_cutoff [, quiet ]]]

helix_orientation_hbond selection [, visualize [, cutoff [, quiet ]]]

loop_orientation selection [, visualize [, quiet ]]

cafit_orientation selection [, visualize [, quiet ]]

angle_between_helices selection1, selection2 [, method [, visualize [, quiet ]]]

Example

fetch 2x19
select hel1, /2x19//B/23-36/
select hel2, /2x19//B/40-54/

# just calculate/visualize orientation of single alpha-helix
helix_orientation_hbond hel1

# get angle between two helices
angle_between_helices hel1, hel2
angle_between_helices hel1, hel2, method=1
angle_between_helices hel1, hel2, method=2

# get angle between beta-sheets
select sheet1, A/47-54/
select sheet6, A/146-149/
angle_between_helices sheet1, sheet6, method=loop_orientation
angle_between_helices sheet1, sheet6, method=cafit_orientation

Output:

PyMOL>angle_between_helices hel1, hel2, method=cafit_orientation
Using method: cafit_orientation
Angle: 145.08 deg

The Script

'''
(c) 2010 Thomas Holder
'''

from pymol import cmd, stored, CmdException
from chempy import cpv
import math

def _vec_sum(vec_list):
    # this is the same as
    # return numpy.array(vec_list).sum(0).tolist()
    vec = cpv.get_null()
    for x in vec_list:
        vec = cpv.add(vec, x)
    return vec

def _mean_and_std(x):
    # this is the same as
    # return (numpy.mean(x), numpy.std(x, ddof=1))
    N = len(x)
    if N < 2:
        return (x[0], 0.0)
    mu = sum(x)/float(N)
    var = sum((i - mu)**2 for i in x) / float(N - 1)
    return (mu, var**0.5)

def _common_orientation(selection, vec, visualize=1, quiet=0):
    '''
    Common part of different helix orientation functions. Does calculate
    the center of mass and does the visual feedback.
    '''
    stored.x = []
    cmd.iterate_state(-1, '(%s) and name CA' % (selection),
            'stored.x.append([x,y,z])')
    if len(stored.x) < 2:
        print 'warning: count(CA) < 2'
        raise CmdException
    center = cpv.scale(_vec_sum(stored.x), 1./len(stored.x))
    if visualize:
        scale = cpv.distance(stored.x[0], stored.x[-1])
        visualize_orientation(vec, center, scale, True)
        cmd.zoom(selection, buffer=2)
    if not quiet:
        print 'Center: (%.2f, %.2f, %.2f) Direction: (%.2f, %.2f, %.2f)' % tuple(center + vec)
    return center, vec

def visualize_orientation(direction, center=[0,0,0], scale=1.0, symmetric=False, color='green', color2='red'):
    '''
    Draw an arrow. Helper function for "helix_orientation" etc.
    '''
    from pymol import cgo
    color_list = cmd.get_color_tuple(color)
    color2_list = cmd.get_color_tuple(color2)
    if symmetric:
        scale *= 0.5
    end = cpv.add(center, cpv.scale(direction, scale))
    radius = 0.3
    obj = [cgo.SAUSAGE]
    obj.extend(center)
    obj.extend(end)
    obj.extend([
        radius,
        0.8, 0.8, 0.8,
    ])
    obj.extend(color_list)
    if symmetric:
        start = cpv.sub(center, cpv.scale(direction, scale))
        obj.append(cgo.SAUSAGE)
        obj.extend(center)
        obj.extend(start)
        obj.extend([
            radius,
            0.8, 0.8, 0.8,
        ])
        obj.extend(color2_list)
    coneend = cpv.add(end, cpv.scale(direction, 4.0*radius))
    obj.append(cgo.CONE)
    obj.extend(end)
    obj.extend(coneend)
    obj.extend([
        radius * 1.75,
        0.0,
    ])
    obj.extend(color_list * 2)
    obj.extend([
        1.0, 1.0, # Caps
    ])
    cmd.load_cgo(obj, cmd.get_unused_name('oriVec'), zoom=0)

def cafit_orientation(selection, visualize=1, quiet=0):
    '''
DESCRIPTION

    Get the center and direction of a peptide by least squares
    linear fit on CA atoms.

USAGE

    cafit_orientation selection [, visualize]

NOTES

    Requires python module "numpy".

SEE ALSO

    helix_orientation
    '''
    visualize, quiet = int(visualize), int(quiet)
    import numpy
    stored.x = list()
    cmd.iterate_state(-1, '(%s) and name CA' % (selection),
            'stored.x.append([x,y,z])')
    x = numpy.array(stored.x)
    U,s,Vh = numpy.linalg.svd(x - x.mean(0))
    vec = cpv.normalize(Vh[0])
    if cpv.dot_product(vec, x[-1] - x[0]) < 0:
        vec = cpv.negate(vec)
    return _common_orientation(selection, vec, visualize, quiet)

def loop_orientation(selection, visualize=1, quiet=0):
    '''
DESCRIPTION

    Get the center and approximate direction of a peptide. Works for any
    secondary structure.
    Averages direction of N(i)->C(i) pseudo bonds.

USAGE

    loop_orientation selection [, visualize]

SEE ALSO

    helix_orientation
    '''
    visualize, quiet = int(visualize), int(quiet)
    stored.x = dict()
    cmd.iterate_state(-1, '(%s) and name N+C' % (selection),
            'stored.x.setdefault(chain + resi, dict())[name] = x,y,z')
    vec = cpv.get_null()
    count = 0
    for x in stored.x.itervalues():
        if 'C' in x and 'N' in x:
            vec = cpv.add(vec, cpv.sub(x['C'], x['N']))
            count += 1
    if count == 0:
        print 'warning: count == 0'
        raise CmdException
    vec = cpv.normalize(vec)
    return _common_orientation(selection, vec, visualize, quiet)

def helix_orientation(selection, visualize=1, sigma_cutoff=1.5, quiet=0):
    '''
DESCRIPTION

    Get the center and direction of a helix as vectors. Will only work
    for helices and gives slightly different results than loop_orientation.
    Averages direction of C(i)->O(i) bonds.

USAGE

    helix_orientation selection [, visualize [, sigma_cutoff]]

ARGUMENTS

    selection = string: atom selection of helix

    visualize = 0 or 1: show fitted vector as arrow {default: 1}

    sigma_cutoff = float: drop outliers outside
    (standard_deviation * sigma_cutoff) {default: 1.5}

SEE ALSO

    angle_between_helices, helix_orientation_hbond, loop_orientation, cafit_orientation
    '''
    visualize, quiet, sigma_cutoff = int(visualize), int(quiet), float(sigma_cutoff)
    stored.x = dict()
    cmd.iterate_state(-1, '(%s) and name C+O' % (selection),
            'stored.x.setdefault(chain + resi, dict())[name] = x,y,z')
    vec_list = []
    count = 0
    for x in stored.x.itervalues():
        if 'C' in x and 'O' in x:
            vec_list.append(cpv.sub(x['O'], x['C']))
            count += 1
    if count == 0:
        print 'warning: count == 0'
        raise CmdException
    vec = _vec_sum(vec_list)
    if count > 2 and sigma_cutoff > 0:
        angle_list = [cpv.get_angle(vec, x) for x in vec_list]
        angle_mu, angle_sigma = _mean_and_std(angle_list)
        vec_list = [vec_list[i] for i in range(len(vec_list))
                if abs(angle_list[i] - angle_mu) < angle_sigma * sigma_cutoff]
        if not quiet:
            print 'Dropping %d outlier(s)' % (len(angle_list) - len(vec_list))
        vec = _vec_sum(vec_list)
    vec = cpv.normalize(vec)
    return _common_orientation(selection, vec, visualize, quiet)

def helix_orientation_hbond(selection, visualize=1, cutoff=3.5, quiet=0):
    '''
DESCRIPTION

    Get the center and direction of a helix as vectors. Will only work
    for alpha helices and gives slightly different results than
    helix_orientation. Averages direction of O(i)->N(i+4) hydrogen bonds.

USAGE

    helix_orientation selection [, visualize [, cutoff]]

ARGUMENTS

    cutoff = float: maximal hydrogen bond distance {default: 3.5}

SEE ALSO

    helix_orientation
    '''
    visualize, quiet, cutoff = int(visualize), int(quiet), float(cutoff)
    stored.x = dict()
    cmd.iterate_state(-1, '(%s) and name N+O' % (selection),
            'stored.x.setdefault(resv, dict())[name] = x,y,z')
    vec_list = []
    for resi in stored.x:
        resi_other = resi + 4
        if 'O' in stored.x[resi] and resi_other in stored.x:
            if 'N' in stored.x[resi_other]:
                vec = cpv.sub(stored.x[resi_other]['N'], stored.x[resi]['O'])
                if cpv.length(vec) < cutoff:
                    vec_list.append(vec)
    if len(vec_list) == 0:
        print 'warning: count == 0'
        raise CmdException
    vec = _vec_sum(vec_list)
    vec = cpv.normalize(vec)
    return _common_orientation(selection, vec, visualize, quiet)

def angle_between_helices(selection1, selection2, method='helix_orientation', visualize=1, quiet=0):
    '''
DESCRIPTION

    Calculates the angle between two helices

USAGE

    angle_between_helices selection1, selection2 [, method [, visualize]]

ARGUMENTS

    selection1 = string: atom selection of first helix

    selection2 = string: atom selection of second helix

    method = string: function to calculate orientation {default: helix_orientation}
             or int: 0: helix_orientation, 1: helix_orientation_hbond,
                     2: loop_orientation, 3: cafit_orientation

    visualize = 0 or 1: show fitted vector as arrow {default: 1}

SEE ALSO

    helix_orientation, helix_orientation_hbond, loop_orientation, cafit_orientation
    '''
    visualize, quiet = int(visualize), int(quiet)
    methods = {
        '0': helix_orientation,
        '1': helix_orientation_hbond,
        '2': loop_orientation,
        '3': cafit_orientation,
    }
    methods.update((x.__name__, x) for x in methods.values())
    try:
        orientation = methods[str(method)]
    except KeyError:
        print 'no such method:', method
        raise CmdException
    if not quiet:
        print 'Using method:', orientation.__name__
    cen1, dir1 = orientation(selection1, visualize, quiet=1)
    cen2, dir2 = orientation(selection2, visualize, quiet=1)
    angle = cpv.get_angle(dir1, dir2)
    angle_deg = math.degrees(angle)
    if not quiet:
        print 'Angle: %.2f deg' % (angle_deg)
    if visualize:
        cmd.zoom('(%s) or (%s)' % (selection1, selection2), buffer=2)
    return angle_deg

cmd.extend('helix_orientation', helix_orientation)
cmd.extend('helix_orientation_hbond', helix_orientation_hbond)
cmd.extend('loop_orientation', loop_orientation)
cmd.extend('cafit_orientation', cafit_orientation)
cmd.extend('angle_between_helices', angle_between_helices)